杨川，上海金融与发展实验室特聘高级研究员

上文回顾

上文重点介绍了“基础估值”的概念和假设。基础估值是一个项目在投资人的必要收益率（即最低折现率）和动态投资回报期要求下，得出的价值或投资价格。基础估值与传统估值方法不同之处就是加入了时间要素。

本文关于时间要素对估值影响的研究，相较于传统估值方法有三大重要突破：一是“有效价值期”，这个概念是对DCF方法中戈登模型的颠覆，即估值不存在永远增长的永续价值，存在“估值终点”。二是“隐含终值的动态回收期”，这个概念是通过对历史价格下动态回收期的分析，发现了所有价格或估值的投资回收期都隐含了终值（或投资期末余值），这种隐含就是市场对未来模糊性的拥抱，隐含终值比那种毫无根据的假设终值更有意义，因为它就是市场对远期的预期。三是“投资效率”，传统估值理论中，折现率就是一个与投资回收期无关的资本利率（资本成本），因此传统估值方法是不考虑回收期等投资效率的，而现实中投资回收期至关重要，因为在估值和资本成本不变的情况下延长投资回收期，相当于是投资价值的折损。因此，通过投资回收期的对比分析，可以量化估值或价格的泡沫程度。这对无论是PE/VC的股权投资，还是股票投资都具有非常现实的实用价值。

成长性驱动价值模型（续）

八、估值难点：时间要素

时间是估值中与折现率同样重要的变量。很多估值方法，或者使用这些方法的人，都没有区别可预测期与投资期限，对投资期后的终值估值更是束手无策。比如，DCF方法就是假定投资期限为无限期，终值也是靠戈登模型的假设来评估；退出倍数法，直接用投资期，而非可预测期，期末终值就是投资期外的价值，对期末终值的评估也是使用期初可比同类企业的市盈率的假设。这两种方法中的假设都是不合理和没有依据的假设。因此非常有必要深入了解预测期限和期末余值概念，以及隐含终值的动态回收期（Dynamic Payback Period，DPP）等概念，才能走出上述一系列估值的误区。

1、预测期

预测期是投资人通过广泛和深入地信息收集与分析，获得了一个可以对项目评估的大致评估周期。比如，对医药项目的评估，首先要获取从动物实验到临床实验的关键信息，评估新药从动物实验到临床实验成功的时间周期，以及这个新药获批上市后直至专利过期的时间周期，然后根据不同阶段关键信息模糊度的大小，来调整该期间的折现率高低，再按照不同阶段的折现率对盈利预测进行估值。

预测期相当于是终值前的时间段，也就是信息黑箱前的可预测阶段。因此，通常预测期要长于投资期。换句话说，一项理性投资的投资期限不可能长于可预测期。

由于传统估值方法对预测期和投资期限没有明确加以区分，即便达莫达兰的两段估值方法，也没有做区分，因此就出现了对期末终值（TV）使用的歧义：终值究竟是投资期期末，还是信息明确期期末，还是预测期期末？比如一个项目，投资期限是2年，预测期是8年，前5年的预测值比较有把握，后3年的预测值具有较大的不确定性，因此折现率高于前5年，8年以后进入信息模糊阶段，不确定性和折现率又比前3年大幅增加。那么在预测终值时，是2年后的价值，还是5年后的价值，还是8年后的价值？用这三个期限做出的估值结果会完全不同。

应该说，在考虑了信息模糊度下的风险折现率与资本的时间风险折现率后，用8年末的终值更合理，其次是用5年末的终值，最不合理的是用2年末终值。因为第2年后还有可靠的预测数据没有用于价值评估。

2、有效价值期

预测期限不可能无限，也不可能过长，每个项目都有其固定的“有效价值期”，预测期只能在有效预测期内（预测期≤有效价值期）。有效预测期是在投资估值或交易价格下，其盈利的内部收益率大于或等于投资折现率（即IRR≥R）的期限。因为随着预测期限延长，一旦企业产品竞争优势不再，或者增长基数扩大，导致增长率下降，使得IRR开始下降，而R却会随着时间上升，当IRR开始小于R后，净利润的现值NPV或CPV会为负值。换句话说，不存在永续价值，预测时点会终止于下降的IRR曲线与上升的R曲线相交的时刻，见下图：

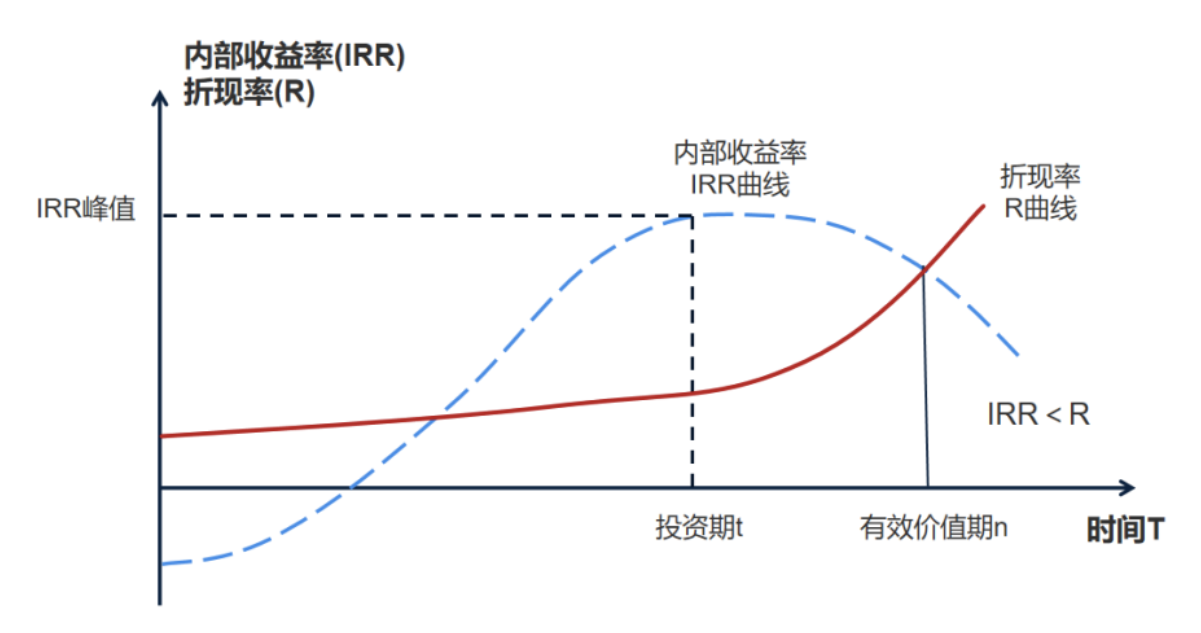
图1.内部收益率/折现率-时间曲线示意图

图1为投资内部收益率（IRR）和折现率R的时间曲线示意图。其中的R曲线会随着时间的延长呈上升趋势，尤其在预测期后，随着信息不确定性的急剧增加，R曲线会陡峭上升，原因前文分析过，一是资本的时间风险溢价（Horizon Premium），另一个是信息模糊度增加，导致折现率大幅上升。

上图是大多数企业的特征，当然，也存在像标普500前十名中的科技巨头一样的长期增长型企业，这类企业因内部持续创新能力。或者不断并购外部创新资源，会不断涌现出增长的“第二曲线”，从而推高IRR曲线，延长了有效价值期。因此，我们创建“成长性驱动价值模型（Growth-Driven Value Model，GDVM）”的目的之一，也是要找到产生“第二曲线”的价值动力源。

3、投资期限

投资期限（Investment Horizon）分为持有期（Holding Period），静态投资回收期（Static Payback Period，SPP）和动态回收期（Dynamic Payback Period，DPP）。SPP是不考虑货币时间价值和投资风险收回本金的时间；DPP是考虑货币的时间价值与投资风险的回收期，即按照投资人必要收益率（Required Rate of Return, RRR）收回本金的时间。RRR也是一项投资的折现率（R）。以DPP为投资期限的估值就是“基础估值”。投资期限可以超过DPP，也可以在DPP内，这两种情况的估值结果是不一样的。

在股票市场中，任何一个时点的价格都是所有投资人按照各自的价值与风险预期，通过交易形成的均衡价格。买入者有短期投机者，也有长期持有者，他们各自的目标价位也不同。我们可以通过对历史价格与后期的盈利情况分析，得到不同风险水平（R）下不同的动态投资回报期（DPP），或相反，不同DPP下不同的R。这个历史价格下的R-DPP关系，可以为当下的估值提供重要依据。比如可以根据最新的信息，在这个历史依据的基础上进行调整，从而得到比较准确的评估结果。这种方法摆脱了传统估值方法中依赖各种没有依据的假设，来做“Garbage In, Garbage Out”的所谓“精准估值”的弊端。

4、投资回收期

必要收益率R其实是资本成本，而非真实的收益率，比如年化收益率r。因为通过R推不出每年应该盈利多少？按照必要收益率R也推导出不出动态投资回收期DPP，那么就有一个深刻的问题：在同样的估值P和相同的风险水平（即必要收益率R）下，增长率g越低，DPP就会越长，而延长了DPP虽然没有降低必要收益率R，但其实降低了年化收益率。换句话说，降低了投资效率。

尽管投资回收期是评估投资效率的基本指标，但在国际主流学术研究和实务应用中，其地位远低于NPV和IRR。根据2025年最新研究数据，超过78%的学术论文和82%的企业投资决策报告中，将NPV作为核心评估指标，IRR作为次核心指标，而回收期法仅在27%的文献和19%的企业报告中被提及。这种关注度差异主要源于以下原因：

计算简便性与决策效率的权衡：回收期法计算简单直观，但仅关注资金回收速度，无法全面反映项目整体盈利能力。

时间价值与长期收益的考量：NPV和IRR全面考虑资金的时间价值和项目全周期收益，而回收期法忽略或部分忽略这一因素。

指标互补性：在存在多重解或规模问题时，IRR可能失效，NPV则更为可靠，而回收期法无法解决这些问题。

这些原因总结很大程度都是认知误区。后面我们在“隐含终值动态回收期”概念中回一一解答产生这些认知误区的原因。

在估值中，静态投资回收期（SPP）和动态投资回收期（DPP）要比持有期更重要。一个项目首先要在SPP收回全部投资本金，其次，在SPP+t的时间内，要收回必要必要收益率（即折现率R）的全部收益，这个SPP+t’就是DPP，t’一般为1-2年。只有在确定了风险偏好R和DPP后，才能确定一个项目的基础估值，然后在基础估值上进行投资期限的调整，计算出超出DPP的持有期投资价值。

因为基础估值的投资期限就是DPP，因此估值首先需要确立DPP。而持有期则会因各种情况发生变化，比如，因项目实际结果不及期初预计而缩短投资期限，提前退出；或者因企业的持续创新能力导致股价上升，而延长投资期限；或者在高位被套牢，需要等待解套机会，不得不延长投资期限。而在估值P和回收期DPP确定后，折现率R与增长率g就存在一个正相关的关系，也就是高风险对应高增长。

DPP是几乎所有估值方法都忽略的一个指标。它其实与折现率（R）一样，都是投资人的必要的投资条件。因为折现率（R）就是必要收益率（RRR），DPP也就是最短的投资回报期。也就是说，DPP是再折现率R下，投资本金收回的时间。因此，在估值时，首先要确定投资人的风险偏好R值，然后就要考虑何时才能收回现值本金？再根据DPP内的盈利，，就可以用估值公式PEGR计算出估值水平（P/E）。

任何一个市场价格，在不同风险水平（资本成本R）下都有着与其对应的动态回收期DPP（最短回报期n），它们之间的关系会形成一个“收益率-时间”曲线图：

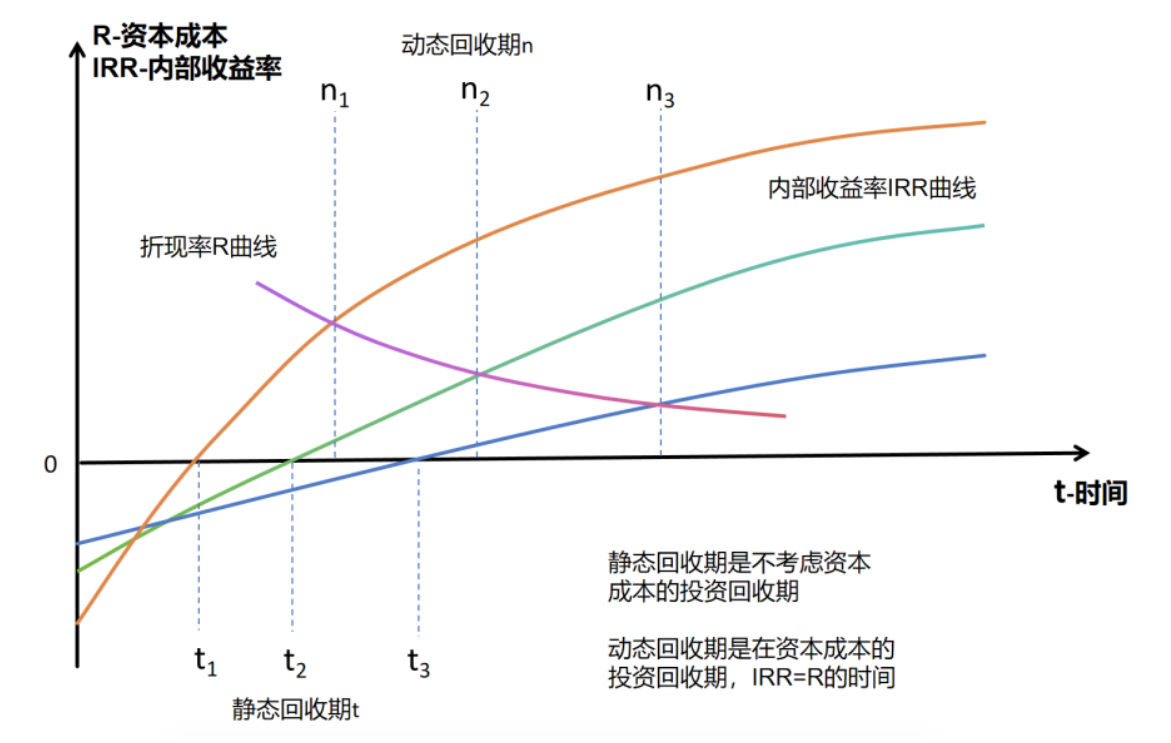
图2.投资静态回收期与动态回收期示意图

如图2所示，R曲线是投资人的风险偏好曲线，IRR曲线是期初价格和期间业绩形成的内部收益率。静态投资回收期（t）不受折现率的影响，但动态投资回收期（n）却受折现率（R）的影响。R曲线如果上移，动态回收期（n）就会延长；反之R曲线如果下移，n就会缩短。

对于科创风险投资来讲，包括高科技的上市公司的股票投资，其高增长会在远期实现，投资人因对其远期愿景的预期乐观，愿意延长投资期限。这样就出现投资期限可以延长的两种情况：（1）风险预期低，可以接受较低的增长率和较长的回报期（比如公共基础设施项目）；（2）未来增长率预期高，可以接受较高的风险预期下较长的投资回报期（比如生物医药项目）。前者是安全换来的较长投资期限；后者是乐观预期换来的较长投资期限。这两种情况都可以通过PEGR公式推演出来。比如在估值不变的情况下，风险预期R下降时，投资人就可以接受一个较低增长率G和较长投资回报期n的项目；同样也可以接受一个较长投资回报期n，但未来高增长的项目。比如评估一个长周期的新药项目，预测期超过10年，正是10年后爆发的高增长价值与长周期的高风险平衡，才形成了早期投资的价格。

总之，我们在估值或分析股价时，一定要关注历史静态投资回收期（SPP）和动态投资回收期（DPP），如果今天估值的SPP和DPP相比最近的历史值发生了较大变化，那么一定是预期发生了变化，比如SPP和DPP都延长了，其背后原因要么是现在的风险水平下降了，要么是对未来盈利增长的预期增加了，或者是价格泡沫出现了。也就是说，投资回收期的变化，往往预示着公司内在价值或风险的变化。投资回收期背后的风险水平、未来预期和价格泡沫都是直接影响投资决策的重要因素，但在传统估值方法中很少有所涉及。

5、隐含终值的投资回收期

在做DPP分析时，往往会出现对DPP的一个普遍误解，即一个项目的可能最大价值不在DPP内，而在DPP外的远期，因此DPP不重要。这种观点只是对DPP的表面理解，实质上，所有估值和价格的DPP，都隐含了远期收益，包含了终值。这一点从历史价格分析就很容易理解，任何一个股票或股权的历史价格，其后来业绩形成的动态投资回收期（“净利润现值之和CPV=初始投资”的时间）都包含了终值，我们称之为“隐含终值DPP”（DPP with Implied Terminal Value，DPP-Implied TV）。

因此，“隐含终值DPP”也表达了价格和估值的本质——“所有市场定价都包含了全生命周期价值”。

股票价格P =预测期净收益现值之和CPV + TV现值

我们在分析历史价格时，形成这个价格的业绩是客观事实，因此历史DPP都是隐含TV的。同样，在用DPP估值时，预测DPP中也隐含了终值TV。

既然DPP包含了两部分：预测期CPV和终值现值，那DPP从时间划分上，也可以分成两段，一段是可准确预测的阶段，另一段是预测期外的终值。这种两断论的方法类似于达莫达兰的DCF两段论模式，但与达莫达兰DCF两断论模式不同的地方，就是DPP隐含的终值不是戈登模型的永续价值假设，而是来自市场预期，只不过市场将这种预期与可预测的业绩预期“融合为一体”，形成了估值或交易价格下的DPP。如果要对这两个时间段做精确分割是不现实的，我们只能将可精准预测（或高确定性业绩）阶段的业绩作为DPP中的第一段价值，剩余部分为终值价值。换句话说终值价值就是预测模糊期的市场预期价值。比如，分析一个DPP为7年的股票价格，前4年业绩为可准确预测期的价值，后3年业绩就是市场预期的终值价值。

隐含终值DPP（DPP-Implied TV）与其说是一种新理论不如说是一个新发现，它揭示了市场价格并非仅反映DPP期间的净利润现值，而是通过“隐含终值”机制，将未来的终值提前计入了回收期内的净利润现值中。因此，隐含终值DPP解决了DCF方法困扰估值实践的戈登模型假设（永远增长、增长率和折现率不变）脱离实际，没有依据，且容易被人为操控（比如增长率2%还是3%结果相差甚巨）等一系列问题。隐含DPP是一种“对市场不确定性的拥抱”，这比戈登模型对不确定性的精确假设更加客观和更有实用价值。

6、估值的时间约束：投资效率

传统估值方法忽略了价值评估的三大要素：趋势判断、认知差异和投资效率。

趋势判断：估值并不是盖棺定论地一次性估算出企业的终身价值，而是谨慎、保守地根据已有信息做出初步有限的价值/风险判断，这个判断不仅仅是当下的价值与风险的量化，最重要的是对未来价格趋势的判断。比如未来的上涨或下跌的大致空间，并据此做出投资决策。

认知差异：投资的本质，是赚取与市场不同的认知差。如果所获信息和认知与市场无异，最多只能获得与市场相同的收益，那不如直接买ETF指数基金。所有超额投资收益，都来自与市场不同的认知差，或者运气。运气不会永远伴随，运气得到的，终将会凭认知失去。

投资效率：投资效率就是要在必要收益率或折现率（R）下，要有一个投资回收期（隐含终值DPP）的时间约束。然而，多数传统估值方法和指标如DCF模型和P/E、P/S指标都没有时间约束。DCF模型中的时间就是预测期加永续期的企业全周期，其估值要素就是现金流和折现率；P/E和P/S等指标也没有时间约束，比如80倍市盈率与8倍市盈率之间是一个什么关系？投资回收期多长？这些指标都无法解答。

DCF方法中为必要收益率的折现率R与静态投资回报率不同，后者是静态回收期SPP的倒数，而折现率R与动态回收期DPP没有任何关系。R本质上是资本成本（Cost of Capital）或资本的风险利率，它并非投资者实际能获得的年化收益率。因此，折现率是没有时间约束的。DCF方法中的NPV 指标本身不带时间维度，只回答“值不值”，不回答“等多久”。

一个项目 NPV=+1 000 万，可能是 3 年回收，也可能是 10 年回收，数值上完全一样，“多久才能回本”这件事 NPV 既不管、也看不出来。

DCF估值模型的最终落脚点是价值本身，即净现值NPV。这个方法认为NPV可以回答“一个项目能为我创造多少绝对财富”的问题，但它不回答“我需要多长时间才能收回成本”的问题，它认为投资回收期只是用来衡量的是资本流动性的指标。然而，股东是要关心投资效率的，投资效率不仅仅是一个资本的流动性问题，而是风险和回报率的问题：从风险角度，回收期时间越长，不确定性越大，投资风险越高；从回报率角度，一个较短回收期的项目，在延长回收期后可能会获得更高的回报，或者投资其他高回报项目从而获得比较长回收期项目在同时间内更高的投资回报。

显然，传统主流方法又出现了一个巨大的Bug——如果没有时间约束，“一个项目能为我创造多少绝对财富”的问题，究竟是投资回收期是3年，5年，还是10年？尤其是我们在使用“隐含终值回收期”后，所谓DPP后的价值评估也就没有意义了，因此DPP就成为了投资效率的重要参数。

除了DPP，投资期限不同，投资回报也完全不同。一个项目，如果在DPP后期增长率不变，或者下降幅度不大，能够保持投资的内部收益率IRR不低于折现率R，延长投资期就会增加投资回报。比如2019年投资英伟达，在投资期两年后，发现其增长率并未下降，就可以延长投资期，比如至五年，五年的回报率就会比原计划两年大很多。因此，时间要素是衡量投资回报的核心指标，需要纳入估值体系。

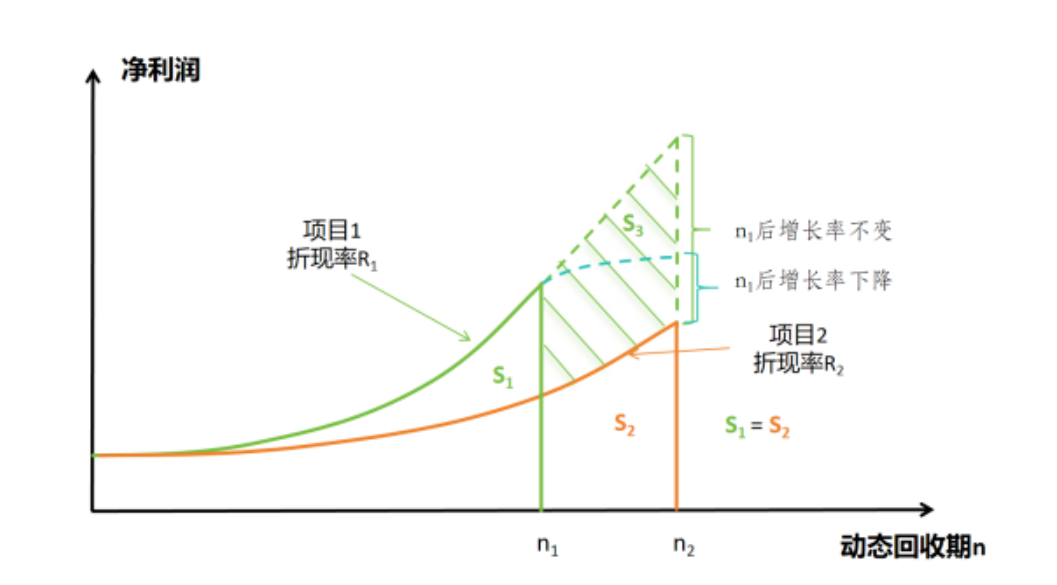
图3.相同估值不同动态回收期的价值比较

图3是相同估值下两个不同DPP项目的比较，S是项目的净现值面积，因为估值相同，两个项目在DPP期内的净现值面积相同（S1=S2）。项目1在动态回收期n1期后，如果增长率不变，或增长率虽有下降，但仍然IRR≥R，项目1的投资期限延长至项目2，会增加S3面积的净现值，因此，两个项目虽然估值相同，但价值完全不同，我们把这种比较称之为“等效价值比较”，即在同等投资效率下（即同样DPP下），两个项目价值的比较。

围绕“等效价值比较”，我们可以建立一个新的估值指标：投资效率（Investment Efficiency，IE）。IE就是按照给定风险水平R，在DPP期间内实现的投资回报（净现值之和CPV）与DPP的比率：

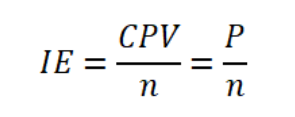
其中，n为动态投资回收期（隐含终值DPP）。

这个公式非常简洁，它可以直观地比较相同估值下不同DPP 项目的投资效率。相比投资回报率ROE、NPV和内部收益率IRR等传统评价指标，IE更加简洁和方便，更有助于投资人快速做出估值比较与投资决策。

IE的使用方法：在比较两个估值相同但DPP不同的项目时，可以通过“等效价值比较”（即同等投资效率下的价值比较），来计算“等效差值”。等效差值就是按照相同的初始投资P，采用DPP较长项目的时间，通过投资效率IE来计算DPP较短项目的价值，这个价值与较长DPP项目的价值之差。

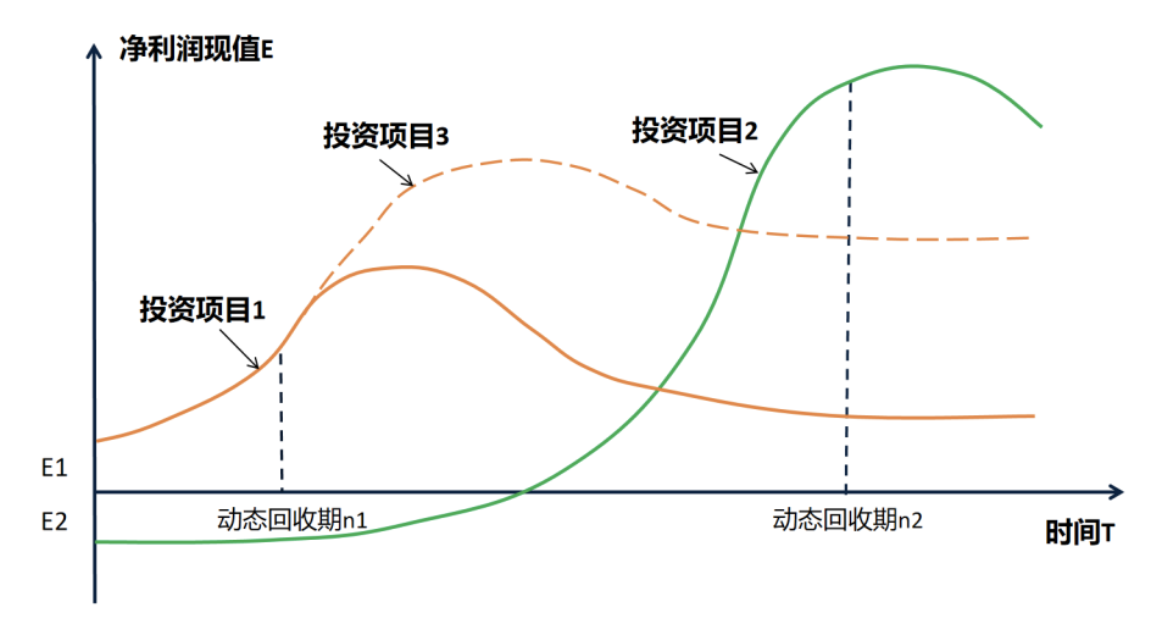
图4.投资效率比较示意图

如图4，项目1为当期盈利且快速增长的项目（比如苹果公司）；项目2为前期亏损（E2为负值），但后期会有陡峭增长的项目（比如特斯拉）。因为n1＜n2，因此，如果延长投资项目1的投资期限到n2，投资回报显然会增加，增加有两种方式：一是延长在项目1的持股期；二是投资回报率较高的项目3。由于n1后的各种选择的项目价值增长曲线不同，可以用线性增加的方法简化这种比较。因此在做项目1与项目2的等效价值比较时，就用n2×E1=n2×P1/n1来与P2进行比较。比如：项目1的投资为P1=1000万，n1=5年，IE1=200万/年；项目2的投资为P2=1000万，n2=10年，IE2=100万/年，与项目2等效的项目1的价值为10×200=2000万，等效差值为2000万-1000万=1000万。这说明项目2不及项目1，其价值差为1000万。也就是说，同样估值的项目，如果DPP很长，就需要更高的投资价值才能与较短DPP项目的价值等效。同样估值的两个项目，DPP长的项目要么盈利增加，要么就必须估值下降。

总结：IE指标是一种在同样估值或价格下，进行等效价值的比较的便利工具。它通过模拟相同条件下（按照较长DPP时间），两个或者多个项目的等效价值，做比较和筛选。IE指标有以下几点其他估值方法所不具备的优势：

（1）同量纲可比

IE比率结果消除了不同投资项目之间的项目规模差异（取同样估值或投资额）、投资期限差异（不论投资期限，只比DPP），初始利润差异（不管初始利润大小），估值水平差异（不论P/E大小），以及项目折现率和增长率等指标的差异，简单、直接地对不同项进行比较。相比之下，ROE、NPV指标都不包含时间因素，也看不出表达投资效率的等效价值，更无法做跨项目的比较。

（2）全生命周期价值比较

动态回收期（DPP-Implied TV）是“IRR=R”的投资回报期，它包含了终值的全周期价值，因此，就彻底摆脱了“终值假设”。可以方便地跨项目比较和做投资决策。比如，如果要投一个DPP较长的生物医药项目，就知道这类项目在同样估值下，与较短DPP项目的等效差值，然后做出二者的比较和筛选。

（3）有效价值比较

投资效率IE与前文介绍的现值增长率G一样，它们都是表达有效价值的指标。脱离风险水平R的复合增长率g的比较是没有意义的；同样，脱离了时间约束DPP和投资效率IE考量的估值P，对于投资决策也没有意义。

投资本金收不回、退不出是投资的大忌。这个因素如果没有纳入估值体系，就说明传统估值方法存在着包括前文揭示的一系列漏洞与缺陷。这些漏洞和缺陷亟待修正与改革。

7、估值-时间的关系

传统估值体系本质上是一种绝对估值法，达莫达兰的两断论，也是用预测期内价值和期外的终值来评估一个项目的绝对价值。这种绝对价值即没有对价值趋势的判断，也没有投资人与市场的认知差判断，更没有发现投资回收期与投资效率的重要性，也区分不出不同投资期限的投资价值。

总之，对投资期限的模糊以及对投资回收期的忽视是FCF方法的一个很大误区，无数历史案例，以及PEGR公式的结果都证明，不同的投资期限，估值完全不同。

图5.估值/股价与时间关系示意图

图5为一个企业从初创到衰退的生命周期内价值-时间示意图。投资估值并不是一个固定的价值，而是投资期限的函数，比如徐新投资京东的8年至IPO的投资期限，其价值是短期投资2-3年投资期限价值的很多倍。

图5展示了一种投资规律：在成长期(0-t2)，投资期限越长，投资回报率越高，也就是说，在某个项目的DPP后，如果增长率G可以保持投资的内部收益率IRR≥R，长期持有比短期持有的回报率更高，这就是耐心资本的价值投资逻辑。这个逻辑在PEGR模型上表现为估值水平与盈利能力、风险水平和资本耐心的量化关系（见图6）：

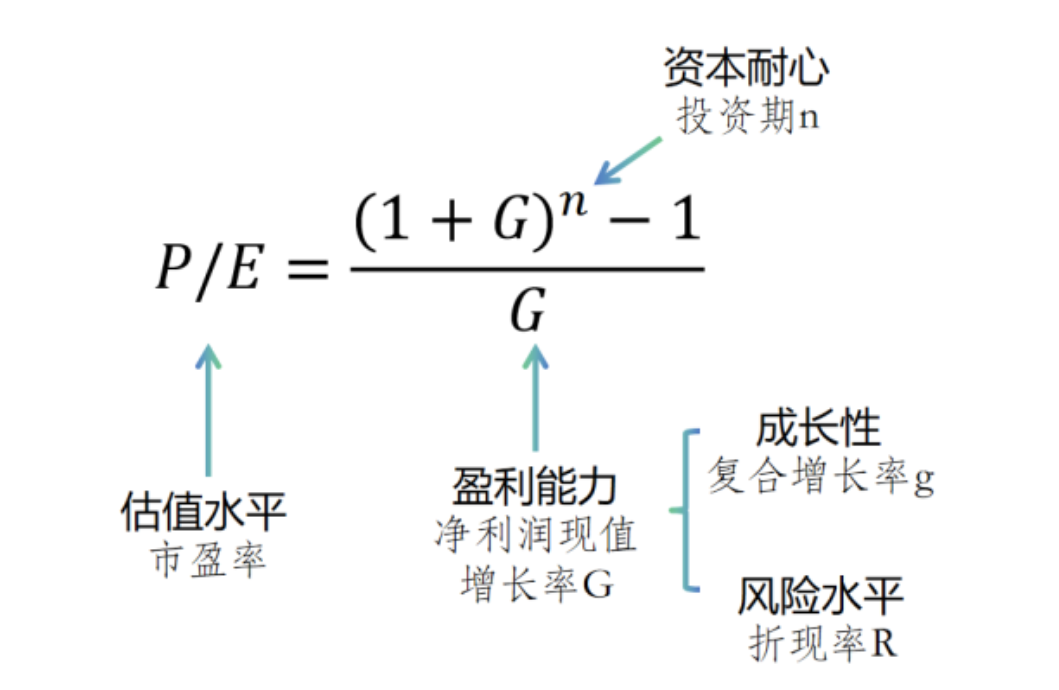
图6. PEGR模型的结构示意图

估值水平（P/E）与成长性（G）和投资耐心（n）呈正相关关系，与风险水平（R）呈负相关关系。这四个变量可以通过已知的三个来确定一个，也可以通过已知的两个，来建立另外两个之间的函数关系，比如在估值水平P/E=30倍，投资期限n=7年的情况下，风险水平R与复合增长率g的关系，假定增长曲线为平滑曲线，复合增长率g与现值增长率G的关系为：G=(g-R)/(1+R)；g=G(1+R)+R。

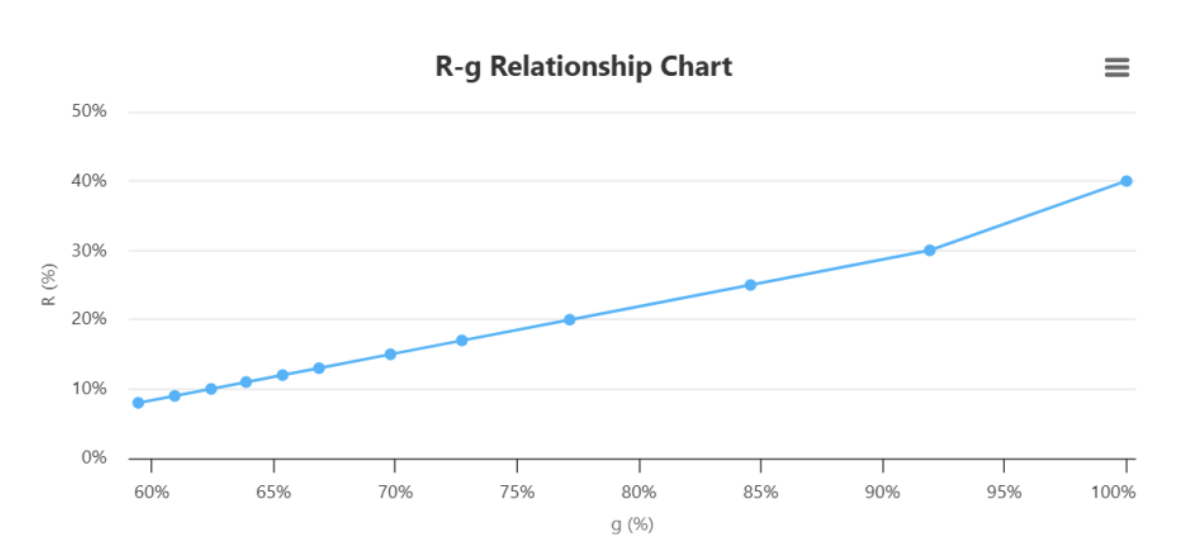
图7. 估值水平和投资期限确定下的折现率与增长率关系的R-g曲线

通过PEGR公式对R-g关系的量化分析（见图7），我们发现，在一个接近平均市场估值水平P/E=30和中等风险R=10%的股票投资上，其7年内的复合增长率要达到g=61%才能维持这个市盈率。考虑到股票的流动性溢价以及“合理泡沫”（即二级市场的“啤酒泡沫”），按照P/E的60%作为真实估值水平P/E=20倍，用PEGR公式计算，其7年内的复合增长率要达到g=47.6%才能维持这个市盈率。

总结：时间要素与增长率和风险水平是同等关键的估值要素，对估值具有决定性影响，而非传统方法中所认为的次要变量。DPP的长短，不仅可以反映市场对预测期外终值的预期，也会揭示出估值是否存在不合理的泡沫。因此，通过参考历史数据并结合对未来增长的合理预估，我们可以将时间要素作为测量工具，来量化价格泡沫化的程度。

（未完待续）

来源：上海金融与发展实验室